Applying Scales and Chords to the Study of Keys
Part II
In Part I of this article series, we illustrated how some of the most basic tools in our musical tool-box could be employed to achieve a functional, foundational understanding of the the concept of ‘keys’ in music. By reinforcing our knowledge of scales and chords and then distilling that knowledge for the purpose of understanding keys, we were able to able to reveal the infrastructure behind keys as a product of the common musical devices we know and use everyday.
To further summarize:
- At the core of all keys is a basic major or minor scale. Everything that occurs within a key will be based on of the notes of that scale.
- We use key signatures at the beginning of pieces to indicate which scale we are using (i.e., which key we are in), and to serve as an abbreviation for accidentals so that we do not need them to be used repetitively throughout the entire piece.
- From our core major or minor scale, we can build a corresponding scale made up of chords (called a chord scale) that we can use as a template for all of the possible basic harmonies we might encounter in the key.
- We can use a system of Roman numerals to simultaneously name and analyze the different chords of the key based on their relationship to the tonic triad.
- Finally, for any of this to make sense, we must understand that the aforementioned components of keys are all bound together in a relationship of functionality, which means that all of the components of a key (scale, chords, etc.) are connected. The highest priority relationship among these is that between the Dominant (V) chord and the Tonic (I) chord, which is exemplified in the musical feeling of ‘arrival’ we find in cadences.
In this article “Discovering Keys: Applying Scales and Chords to the Study of Keys, Part II,” we will further establish our groundwork understanding of keys by delving more deeply into the variations we can find within them, exploring when an anomaly within a key is simply an innocent bit of ornamentation or an indication of impending change, and by taking a brief look at what it means to change keys and what that process can entail.
Really, It’s All About The Sound…
Before we venture any further, it’s important to reinforce that everything we’ve seen and are about to see is derived from sound. Any sort of music theory should be constantly and directly connected with the sound it is endeavoring to explain. Whether we’re talking about the notes on the page or about the theory that is meant to help explain them, if we’re missing the sound, we’re missing the point.
As we’ve mentioned before, the ideal way to be reading these articles is at the keyboard. You will be best served if you are playing or listening to as many of the examples as you can.
Any sort of music theory such as this is meant to be experimented with. Music theorists love partitioning the traits that govern why something sounds a particular way and toying with these traits, examining them, and applying them to different musical scenarios to see how they behave in different contexts. This is largely in contrast with how composer’s tend to write music, which is generally through a combination of study, habit, and creative intuition. However, make no mistake, almost all composers go through some sort of intensive training in music theory. The difference is that composers must practice to apply that theory to the art of composing, and to do so effectively means that the theoretical revelations and principles must become automatic, similarly to the way as performers, we must have an automatic knowledge of the technical aspects of playing our instruments.
Our goal is simply to take a piece of the applied theory that composers and theorists work with to put towards the understanding of something we encounter constantly in music as performers and instrumentalists.
To do that effectively, we need to constantly remind ourselves: music theory = sound.
Look for the Cadences
When we boil it down, we can point to three identifying templates for the sounds of a key. Two of them, scales and chord scales, we covered extensively in our last entry in this series, while the third template we touched on towards the end. We will now spend a moment to reinforce that third feature, cadences.
To find cadences, we must have identified the Dominant (V) chord and the Tonic (I) chord of a scale. In the key of C Major, for example, this would be the G chord and the C chord respectively. Having done this, we can now locate and identify places in the music where these two chords meet in musical union. As mentioned in our last article, V-chords really like to go to I chords, so this occurrence will likely be often.
Just as a refresher, let’s take a quick look at the chord scale and cadence examples from the previous article:

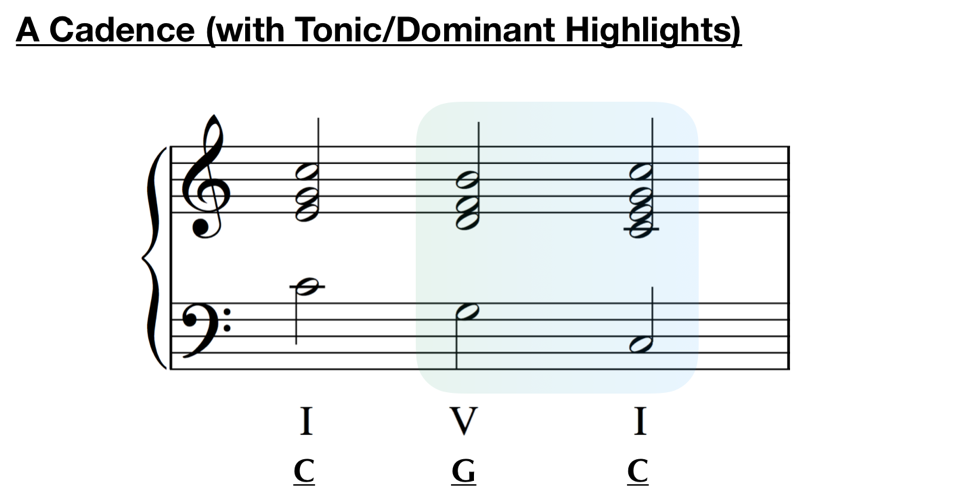
Cadences will almost never be so simply exhibited in music like the second example seen above, however the sound of the cadence is so prevalent and so important to most music built using keys, that composers from eras past often employed cadential templates for writing many of their cadences. These were used, as much as anything, so that the listener would have an easier time following the arrival of a cadence and, in doing so, be more easily able to follow the form of the piece.
Below are examples of some cadences as they are commonly found in the music of their associated composers. Try to play each one and listen for the similarity between their sounds despite the differences in their notation:



Can you figure out which key these cadences are taking place in? (Hint: be aware it may not be the key of the key signature…)
Note as well that cadences need not contain all of the notes of their corresponding chords to be effective. For example, the Bach excerpt above still so very much possesses the sound of a cadential arrival, but only uses a line of two notes to achieve that sound.
As we can see, cadences can also come in a number of different varieties, all of which are meant to play with that feeling of potential energy we get when one occurs. For example, in the Chopin excerpt featured above, we have the cadential chords all present and working, but they are spaced in such a way as to almost feel like the momentum they might have fades out before we can realize their potential in the sense of a more traditionally spaced cadence.
Let’s look at a different kind of example of this. At the end of our Mozart sonata excerpt, we see what’s known as a Half Cadence, whereby there is a distinct and extended landing on the V chord at the end of the phrase. This was often used by composers of the era to change into the key of the V chord after the end of an opening section. Smaller versions of half-cadences were often used to combine two phrases into a larger and more well balanced form, which is a common manner of giving music some breath to unfold more naturally.

Now that we have a better sense of what cadences are and how we find them in the music, we can summarize our three main tools for identifying the basic content of keys as follows:
1) The scale of the key.
2) The chord scale (the harmonic content of the key).
3) The presence of cadences (which indicates functionality).
With all of these things in working order, we’re now ready to move on to the big leagues — how to maintain our understanding of keys when faced with notes that are seemingly not part of the key.
Let’s Get Real: Notes Outside of the Key
Beyond the world of basic teaching music and perhaps simple pop, rock, and folk music, it’s actually quite rare to encounter music that does not contain at least some notes that are not found within the key parameters as we’ve established them thus far.
Even in the seemingly uniform C-major-ness of our familiar Mozart example we find a few of these tones making their way into the mix:

While there is no codified term for these notes when described in this context, we can refer to them as non-scale tones.* (*Note: There is an important distinction to make between the concept of non-scale tones, introduced here, and non-chord or non-harmonic tones, which are a primary feature of Western Tonal Theory. While they share similar purposes, non-scale tones reference any tone that falls outside the foundational pattern of the major or melodic minor scales. This is meant to simplify the identification of abnormal tones as they relate to the key in general. Non-harmonic tones are specifically tailored to the the identity of a specific chord, and are based on the musical intent they exhibit in relation to that chord. As an example, the note F occurring in a passage in the key of C-Major is most definitely a proper scale tone in relation to the key, but it is a non-harmonic tone if the chord it’s accompanying in that passage is a C-major chord. Thus the F would be a non-harmonic tone but would still be considered a scale tone.)
Non-scale tones are used for everything from innocent embellishment to dramatic change. Indeed, one of the most important features of traditional Western Classical music is the smooth transition from one key to another within a formal framework. To do this, composers need to strategically suggest the pivot towards a new key by subtly introducing the new accidentals (or removing accidentals) in the initial key without the change sounding too sudden.
Before we get ahead of ourselves, let’s make sure we have a concrete definition for non-scale tones:
- Non-scale tones are any tones/notes that occur within key-based music that do not seem to be a part of the core scale of the key.** (**Special Note: For ease of understanding, we will only be referencing the major keys in this section on non-scale tones. Minor scales, by nature, have a more complicated design in relation to what is and is not considered a non-scale tone. We will address these concepts as they apply directly to minor keys in a later article.)
This is more easily illustrated by giving a few examples. For example, an F# would be a non-scale tone in the key of C-Major, while an Ab would be a non-scale tone in the key of F-Major. These tones very clearly do not fall within the normal boundaries of the C-major scale (C-D-E-F-G-A-B-C) or the F-major scale (F-G-A-Bb-C-D-E-F), and therefore can be considered “non-scale” tones.
While the basics of learning keys may revolve around learning about their component parts, we won’t be able to achieve a deeper understanding of them until we’re able to see those component parts through all of the non-scale tones we might encounter. To do this, we need to know what those non-scale tones might be and how they work.
The Three Kinds of Non-Scale Tones
We will generally encounter non-scale tones as they fall into one (or more) of three categories: embellishing, modulating, or re-harmonizing.
Embellishing non-scale tones are usually chromatic flourishes meant to introduce color and drama to a passage. While they are generally non-functional, meaning that they do not affect the overall identity of the key, they are often integral to the character of the music. Composers such as Mozart and Chopin are famed for the inclusion of embellishing non-scale tones in their passages and runs:



The main feature that distinguishes embellishing non-scale tones from re-harmonizing or modulating non-scale tones is that we never get the sense that we have deviated from the key-center. In other words, if you were to stop the music in the middle of a passage rife with embellishing non-scale tones, you’d likely be able to still identify the home-note of the key without too much trouble.
Modulating non-scale tones occur specifically to help facilitate a key-change, or modulation. They are usually representatives of the new key signature, and will usually (but far from always) show up in spots where the bulk of the previous key can still be present to smooth the transition. For example, if we’re in the key of C-Major and we want to move to the key of F-Major, at some point we’re going to need some Bb’s, but we’ll often see them in a way that makes their presence as unobtrusive as possible.
Below are a few examples of modulating non-scale tones at work:


As you might expect, the difference between modulating non-scale tones and something like embellishing non-scale tones is that the conclusion of a modulation results in a new key-center and a new key-scale.
Before Beethoven, modulations were generally only made to keys in close proximity to the initial key clockwise around the Circle of 5ths. In other words, if you were in C-Major you would generally modulate up to the key of G-Major, which is the next 5th up. Beyond that, composers would experiment with shifting to the relative or parallel minor, modulating further around the Circle before returning to the starting key, or inputting elaborate sequences to throw off the listener (which we speak of more in a moment). That said, for the most part, key changes followed a fairly standard and predictable route.
Then came Beethoven, who spectacularly ruined everything, which we will address further in our final article of this series.
Finally, we have re-harmonizing non-scale tones. These are the most complicated of the bunch, and the ones most closely related to the Schenkerian theory much of this thinking is based upon.
Perhaps the best way to loosely but effectively describe re-harmonizing non-scale tones is to get all Sci-Fi about it:
Pretend that each key is a separate dimension (yes, in the ‘from another dimension,’ sense…). While doing things in our own dimension (that is, the dimension of the key we’re in) is all well and good, sometimes we really just want to spice things up more than we’d normally be able to by only hanging out there. To do this we can sometimes pull notes or harmonies from different dimensions (different keys) to briefly let the sound and effect of that dimension into the one were working with. The key here is that we’re not going fully into that other dimension (into that other key), we’re just borrowing some of its flavor.
Does it at least make some kind of sense?
Let’s look at an example.
By far, the most common form of this type of re-harmonization occurs when we pull the dominant chord of another key into our own to give that dominant-tonic relationship to a chord that is not the tonic chord of our key.
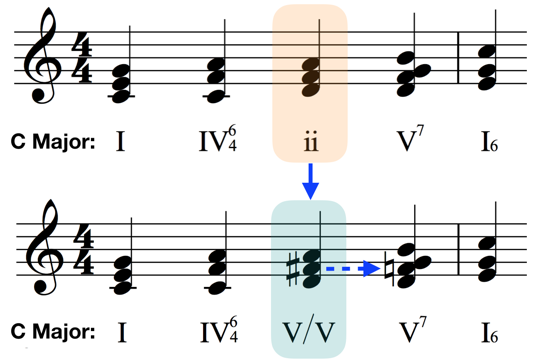
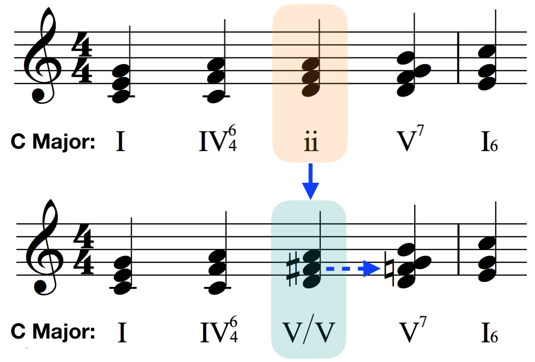
The first of these progressions is a very simple and common progression executed using nothing other than the basic chords of the key, in this case C Major.
The second progression shows our D minor (ii) chord converted to a D major chord, which is now labeled as a ‘V/V,’ which we will explain in a moment.
Play both of these progressions at the keyboard a number of times and really listen for the difference in sound of the altered chord.
Whatever your interpretation of the new sound, we can certainly agree that it adds a flavor that is different than what we’d had in the original progression built using the chords from the key.
What is actually happening here is that we’ve borrowed a chord from a different key to momentarily give us a flavor of that key. In this case, that chord is the dominant (V) chord of the key of G-Major, which is the chord D major. Notice how the progression justifies this change by having a G chord be the next chord in the progression, as though it were part of a regular dominant-tonic cadential progression in the key of G-Major. An important point here is that we don’t actually modulate; this progression is still very much in C-Major, we’ve simply borrowed a chord from another key to give us a different flavor.
These specific kinds of borrowed chords are so prevalent that they actually have their own name, secondary dominants (as in, dominants that are not the primary dominant of the key we’re in). The official way to describe what they do is to say that they briefly tonicize a chord in an initial key with what would be its corresponding dominant in another key. Hence, in the case above, a ‘V’ of ‘V’ (V/V), or a dominant chord of the dominant chord.
Of course we can look at an example!…
Once more, we have two examples below:
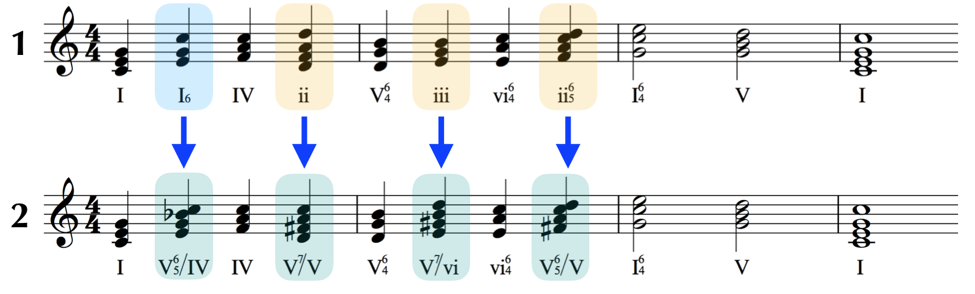
The first is, once again, a standard progression the likes of which we might find in a key that does not deviate any tones from the original key-scale. Pay extra attention to the Roman numerals here.
In the second example, we have almost the same progression, however now certain of the chords have been slightly altered and re-named to reflect the change in their identities to secondary dominants.
Oftentimes the key here is to know that the notes most likely to be altered in these cases are the ‘7’ or ‘ti’ notes of the key-scale we’re borrowing the chord from. That’s because that degree of the scale corresponds to the third of the dominant chord in that key and is a very important identifying note.
Dominants are not the only chords that can be borrowed, however they are the easiest to use and tend to give the most obvious effects, and the notion of borrowing chords from other keys (or substituting chords with those from other keys) finds its way into many different music genres.
Here are a few examples of secondary dominants in action:


So after all of this you may be wondering: What about our Mozart sonata example? What kinds of non-scale tones are those?
Before the answer magically materializes before you, consider the non-scale tone options you’ve just surveyed and listen to the relevant measures in the piece while thinking about which option(s) might be represented in them. Fortunately there are not many altered tones to think about here, but ask yourself, do they seem like embellishing tones, modulating tones, or re-harmonizing tones? Might they be more than one of those options? What does it sound like?
Here is a visual of that passage once more for your convenience:


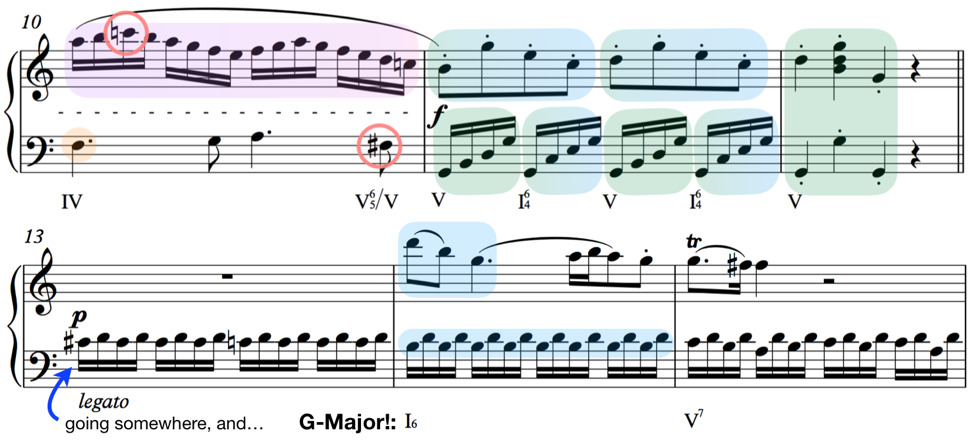
Roman numerals have been provided here only to illustrate easily that yes, we do indeed modulate to the key of G-Major in the succeeding section. Recall how it was common for composers of the time to modulate one step clockwise around the Circle of 5ths to the key of the dominant chord? That is what is happening here.
Are they modulating non-scale tones? Yes.
- Are they re-harmonizing non-scale tones? We conveniently already have the answer to this for the F# in bar ten (which is analyzed as part of a secondary dominant in G major), but what about that C#?
Remember how we talked in the last section about how the non-scale tone accidentals that we usually end up seeing when it comes to re-harmonization are the ‘7/ti’s’ of the new key-scale or the raised thirds of the chords being altered? This, of course, is not always the case, however it’s fairly safe to say that if we see a single outstanding non-scale tone, such as that C# in this Mozart passage, it stands a good chance of being the raised third of a dominant chord from a different dimension, er, key.
If we treat that C# as a raised third of a dominant chord not in the C-major scale, which chord will it be? (Remember how to build thirds and chords from our earlier article on the subject in this series?)
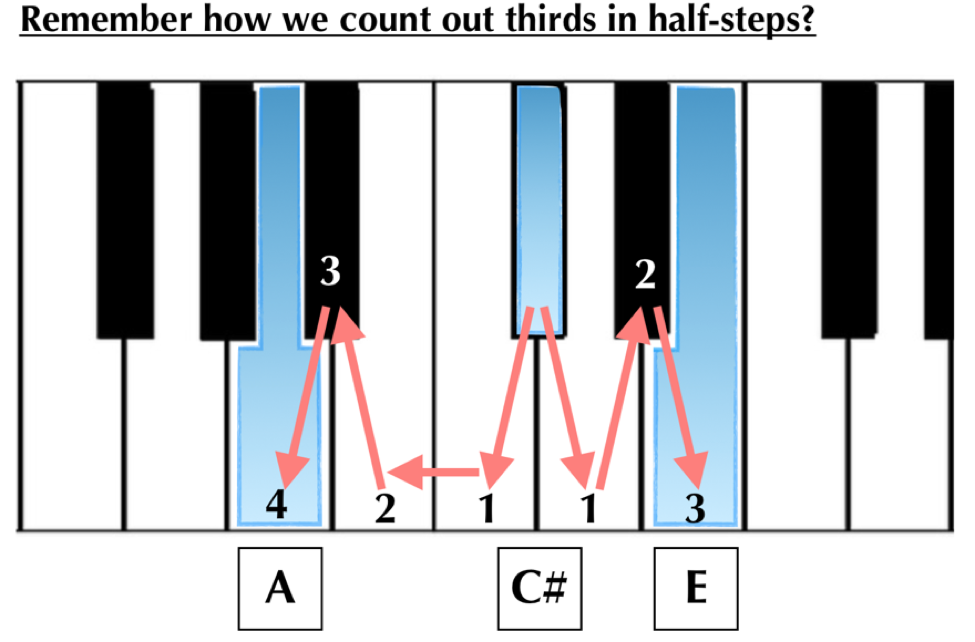
An A-major chord is the dominant (V) chord in the key of D-Major.
If you go back to the Circle of 5ths you’ll see that the key signature for D-Major can be found two notches clockwise from C, and contains the sharps C# and F#. We would have our C# as part of that A-major chord, however what about the F#? By the time we see that it’s most certainly part of a different re-harmonizing (which we’ll speak of in a moment).
As it happens the harmony of D-minor, which is still part of the C-major scale, makes more sense here, and so that’s what we get. The alteration here flies by anyway, and actually has it’s figurative eye on the bigger change to come (the modulation to G-Major).
Now though, looking at that F# in the next measure and the associated,we can apply the same logic to identify it as the third of a D-major chord, which is the dominant (V) chord in the key of G-Major.
So, are they re-harmonizing non-scale tones? Yes.
- Finally, are they embellishing non-scale tones? If we assume that embellishing non-scale tones are the least functionally impactful, than the question here really becomes: Can we live without them?
If you’re able, try to slowly play through this passage as it’s written. Remember, if you can see all of this as simply a variation on the basic C-major scale it will be easier to wrap your fingers around.
Now, try doing so again, but this time play a C instead of a C# in the relevant spot, and an F instead of an F#.
What do you think?
Really, it would take a decently practiced ear to notice that C# and F# had been altered back to their natural state, especially if the piece were played at full speed. Of course, someone familiar with the piece would notice right away, and those with some experience might have a bit of a feeling of ‘off-ness’ from hearing it played like this, however a first time listener would likely think that nothing was amiss. We would still effectively have the modulation to the key of G-Major and, while they might be ever-so-slightly less vibrant, the harmony progressions would still make sense.
You know what that means…
Are they embellishing non-scale tones? Yes.
How Can That Be?
How can we have all three kinds of non-scale tones represented by only two notes in this rollicking but fairly straightforward little section?
The answer is that the notes themselves are only the most visible part of the picture. Much of what justifies their presence is actually occurring around them, in the cascading wash of 16th-notes and the punctuating support of the left-hand bass-notes.
Part of the genius of a great composer is the ability to employ the tools of their craft transparently to achieve a desired goal. By the time we get to these altered notes, the trajectory of the music has already taken us towards the bigger change of G-Major for several measures, without us even knowing it. This is part of the construction of great music, that its design constantly feeds into itself and propels it forward by making its progress seem like an inevitable development of its origins.
And you know what’s worse? Mozart most certainly didn’t even think of it this way. To be sure, he probably chose these notes because they provided the facets of musical artifice we just described, but he did it intuitively, without having to dwell on the why and how, as would likewise be the case with most any practiced composer.
He probably wrote the first 12 measures of this piece in about ten minutes.
Fear not though, part of the reason the theory being discussed in this article series exists is to help us bridge the gap between the capabilities of someone like Mozart and our own efforts. To be sure, there is something to be said for a person’s ‘natural affinity’ for music learning, however the world is full of people who’ve had great successes pursuing musical study as we do here, by reading, internalizing, and naturalizing.
Ok, What Now?
As we’ve seen, the bigger picture of understanding keys contains two main parts: knowing the core components that go into building them, and being able to see those core components through what can often be a variety of intervening material that is not obviously part of the key. To put this more plainly, we need to know the key-scale and key-harmonies, and we need to be able to look beyond all of the various kinds of non-scale tones we might encounter to see the key within.
We will take a bit of a detour to talk about minor keys in our next article, as they require some special attention to effectively combine with what we’ve learned so far.
Then, in our final article in this series, we will put all of our knowledge to the test by looking at analyzing a couple of new passages, with an emphasis on how you might go about doing so at the beginning of learning a new piece. We will also explore a bit into how keys were treated throughout areas of music history, get a small introduction into how keys are treated in jazz, and talk some about how we can continue learning about keys moving forward with our musical training.