What are Chords and How Can They Help Us Learn About Keys?
Chords have been a staple device in the music of the Western world for, well, a long time.
Prior to the Baroque Period (approx. 1600—1750, the musical era of Bach, Handel, and Vivaldi), European music was generally based on linear material, that is to say, on melody. Harmonies, the likes of which we might think of as chords or chord progressions, were the result of multiple melodic lines woven together.
The Baroque Period witnessed the rise in popularity of a simple and effective manner of providing accompanists with harmonic directions called figured bass. In figured bass, a bass line--a series of single notes in the bass-- is accompanied by tiny numbers that indicate harmonic intervals to be played above each note. This was the precursor to the modern shorthand of chord symbols in jazz and pop charts, and it evolved in tandem with the increased inclusion of written chords for keyboard and stringed instruments. Instead of existing as the incidental result of a number of melodies coming together as in Renaissance music, in the Baroque Era, chords finally became an accepted texture unto themselves.

And things only became more, well, chordal from there. From the broken chord figures built into Mozart’s sonatas meant to emulate the strings of an orchestra--to the modern day 12-year old with a guitar who's overjoyed to finally nail the third of those three chords necessary to become a rockstar, the world is virtually chord crazy.
But what is a chord? We can all play them, but can you describe one? Do you really know how chords are made? And more importantly, given that this is an article series dedicated to understanding keys, how can knowing about chords help us learn about how keys function?
As with our previous article, in which we re-built our basic understanding of scales to put towards the greater goal of learning about keys, in this article we will seek out an understanding of chords that gives us both a solid groundwork regarding their construction and identification, and a greater insight into how they function when thinking of keys.
Back to Basics: Chords
First things first though, we need to make sure we have a solid grasp on what chords are and how they’re built.
Let’s dive right in, shall we?
The most simple definition you'll encounter is that a chord happens when two or more notes are played together. This definition might be a little too simplistic, and a better way to define chords goes like this: a chord is a structured collection of notes used in music to convey harmony.
Of course, the explanation only gets more elaborate from there. There are many different kinds of chords to be found in many different musical contexts, and many questions addressing whether something even is a chord versus some other harmonic sonority. For our purposes, however, we’re going to stick to the good ol’ chordal basics as they’ve come to us through the tradition of Western classical music. We’re talking about the kind of chords you find in Schubert lieder, Rachmaninoff preludes, Gershwin rhapsodies, and Billy Joel songs, along with huge amounts of other music both aged and modern.
And we get to start it all off with a nice little metaphor.
Think of chords as being like a tree…

What you’re looking at above is a visual representation of a C major chord with a full complement of extended tones. Don’t worry if this looks a little alien to you, much of what this chord consists of is drawn from more complicated kinds of music, but it’s useful to be able to see how a ‘complete’ version of a chord looks before we go back to see how it’s built from the beginning.
Like a tree, we start with the root note (in red), and grow up through a consecutive series of thirds intervals until we reach the same note two octaves above (the note after the blue A would be a C). Just as scales are built and named by their sequence of steps, chords are always identified by thinking of them in the tightest configuration of thirds that we can, like the image above.
Before we continue any further, let’s remember our thirds on the piano:
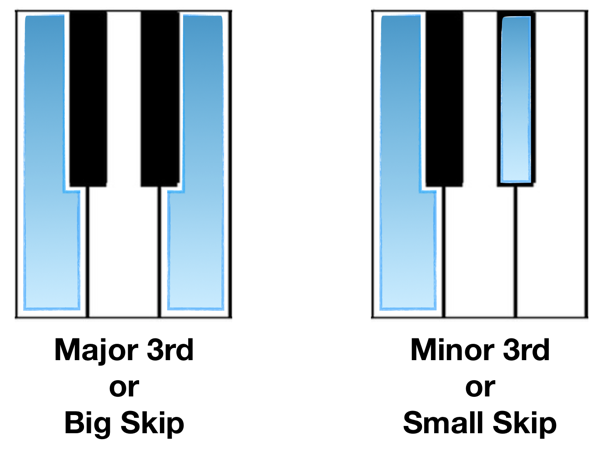
If you play the examples above on the piano, you’ll no doubt hear the ‘happy vs sad’ sound that famously characterizes so much of the music we listen to. This is why the bottom notes of the chord (the ‘trunk’ of the tree, if you will) are the most important. The higher we get, the notes are more colorful and complex, but as they contribute more subtle variations to the sound of the chord, they are often considered less ‘important’ (which is to say, we get the main identity of our chords from the bottom three to four notes.
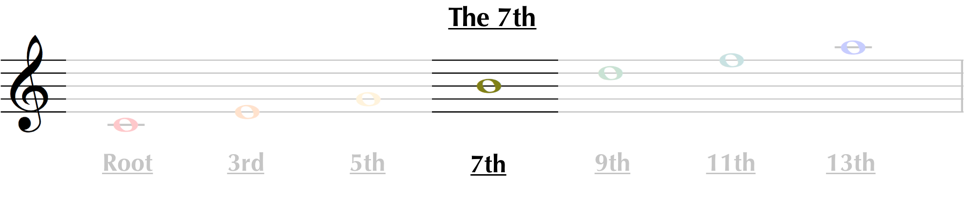
As we build our chord in thirds, we name each new note by its intervallic distance from the root:

If you’re a little concerned that you’re in the wrong classroom, don’t worry; we’re about to simplify things quite a bit. However, being able to see a snapshot of the fuller picture to begin with is often helpful for giving some much needed context to the fundamentals as we learn them.
Besides, it’s all just so pretty…try playing the ‘full chord’ above at the piano (play all the notes together). Listen for the way each note contributes to the combined sound. You may recognize the first three notes as being something you’ve played before: a C Major Chord.
Working backwards, the top three notes of the chord (the 9th, 11th, and 13th) are known as extensions, as they are considered ‘extensions’ of the primary part of the chord.

Extensions are the favorite notes of romantic music, modern classical music, jazz, soul, and other musics that prefer the addition of more complex harmonic contributions.
The center point of the chord going up is referred to simply as the 7th. It serves multiple functions, depending on the circumstances, but is most prevalent as the nearly-necessary addition to dominant 7th chords, which we will learn about in a later article.
Finally, the three lowest notes of the chord make up what we call the triad. ‘Triad’ can refer to any combination of two thirds (see how the top of the chord, the extensions, also seem to make a triad), however for our purposes we will be using the term where it’s most commonly used, in reference to these bottom three notes of the chord: the root, 3rd, and 5th.
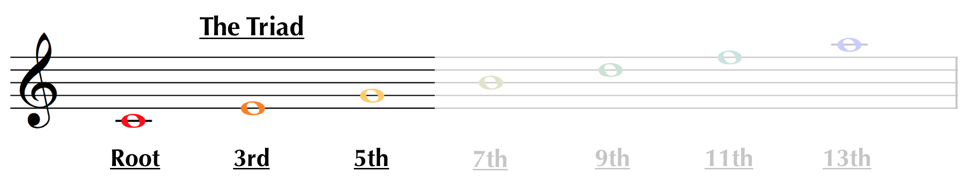

‘Triad’ is the technical term, but from now on we will generally use ‘chord’ as a blanket term to refer to triads and larger chords incorporating 7ths and extensions both, with specifications where necessary.
Counting Chords
Let’s take a look at the C Major Chord on the piano:
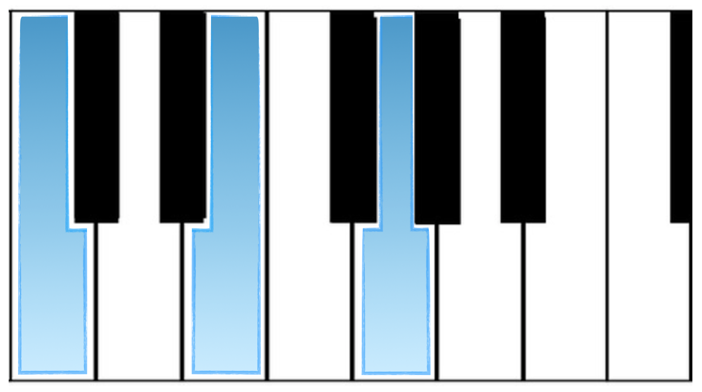
Chords are known and used for their ability to immediately give us a sense of harmonic identity. Need to give a melody some harmonic and textural support? Throw it over some chords. The ease with which this can be done is largely why the classic musical texture of ‘bass-on-the-bottom, harmony-in-the-middle, melody-on-top’ is so prevalent. The real advantage of this comes with our ability to transfer the structure of a chord to many different places across the musical spectrum such that it retains its shape and sound.
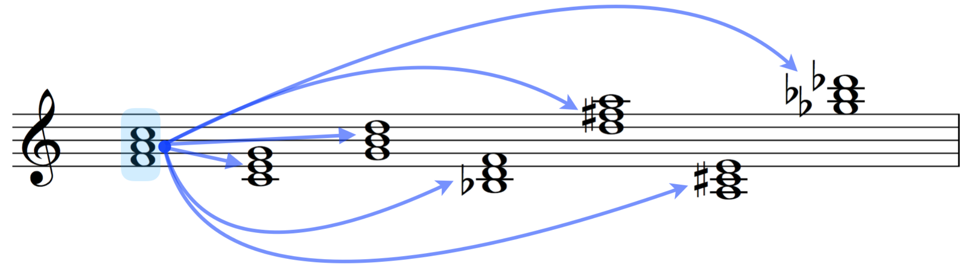
Our C Major Chord will stay a major chord no matter where we move it, as long as we know how to recreate that shape at different spots on the instrument.
That’s where things get a bit tricky, and where we really need to have a solid sense of chord construction to continue.
To build a basic Major chord (a triad) we need to stack two thirds, and we have two ways of counting up to those thirds.
The first way employs a little musical brute force, but it does get the job done...
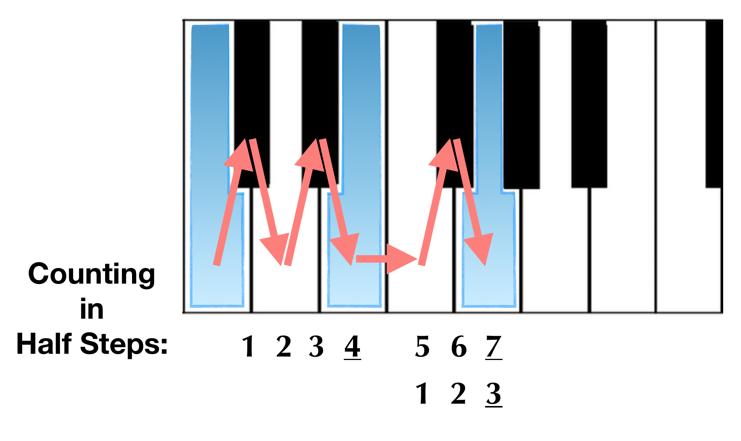
As we can see, using this method entails counting half-steps up until we hit our target notes: C—E (4 half-steps), E—G (3 half-steps). This method can be used anywhere as long as you can remember the number of half-steps that make up major and minor thirds:
Major Third = 4 Half-steps
Minor Third = 3 Half-steps
Remember that you are counting steps using this method, which is different than the way the next method works:
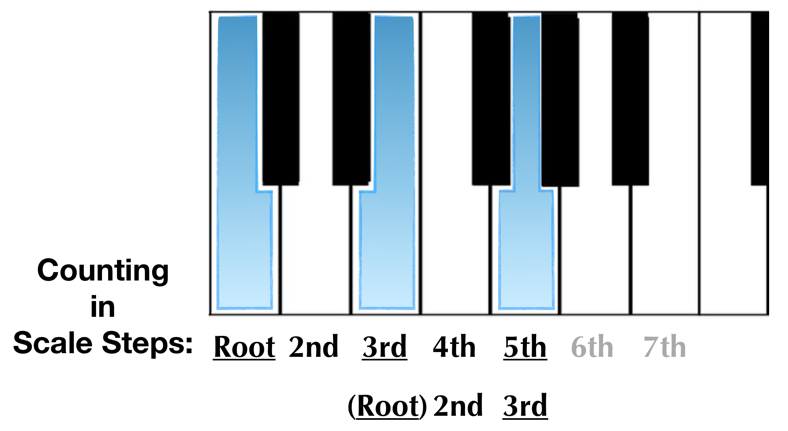
We need a little knowledge of scales to use this method, however it is much more efficient, and much more in line with how we ultimately want to be thinking about both scales and chords.
With this method, we count along the intervals as they ‘grow’ out of the root. Unlike counting half-steps, we count the number of scale degrees to get our interval (not the number of steps), and name the interval after how many scale degrees it is up from the root.
Where we really want to be with our ability to identify thirds and triads is to the point at which we can start to see musical structures (intervals, chords, scales, etc.) as shapes and sounds. Getting there takes a little bit of practice with counting things out, and as much practice as we can get with using our ears to help tell us if things are sounding like they should.
For the sake of practice, see if you can build several major triads using different roots. If you’re feeling really bold, pick your starting notes at random, and see if you can use either of the above methods of counting in combination with your ear to get the right sound.
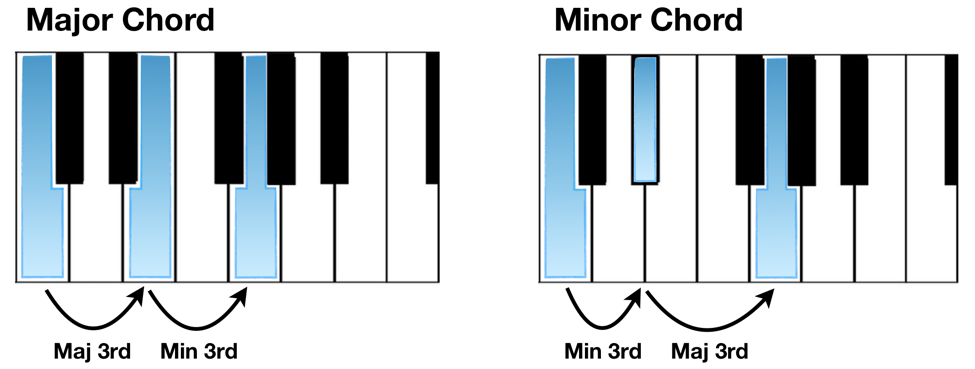
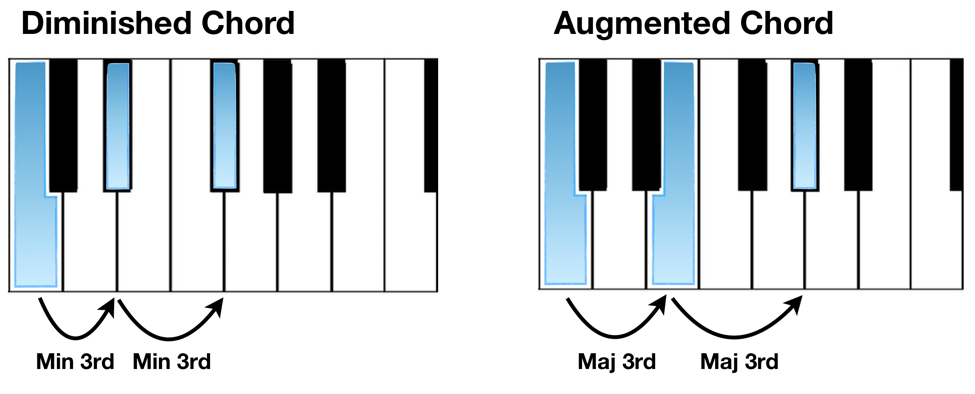
Different combinations of stacked thirds result in different sounds and different chords. The most common are the major and minor variations, but all find their way into many kinds of music in some fashion.
Play them at the piano and listen for their different sound qualities. What kinds of music would you use them for?
After triads, the next most common chord type is the 7th Chord. To create a 7th chord, we stack one more third on top of the two thirds we use to create our triads. Just like with our triads, that third can be either major or minor, and but unlike with our triads, not every version of 7th chord carries the same identifiable heft. That is to say, when in the midst of the music, some 7th chords are going to be more important than others when we consider how the music is built. Some 7th chords come off as more colorful, while others are deeply functional, and the music would be noticeably missing a valuable piece of its forward momentum without them.
We will touch briefly on the most important of these distinctions in our final article on keys, but for right now, let’s take a look at some basic 7th chords on the keyboard:
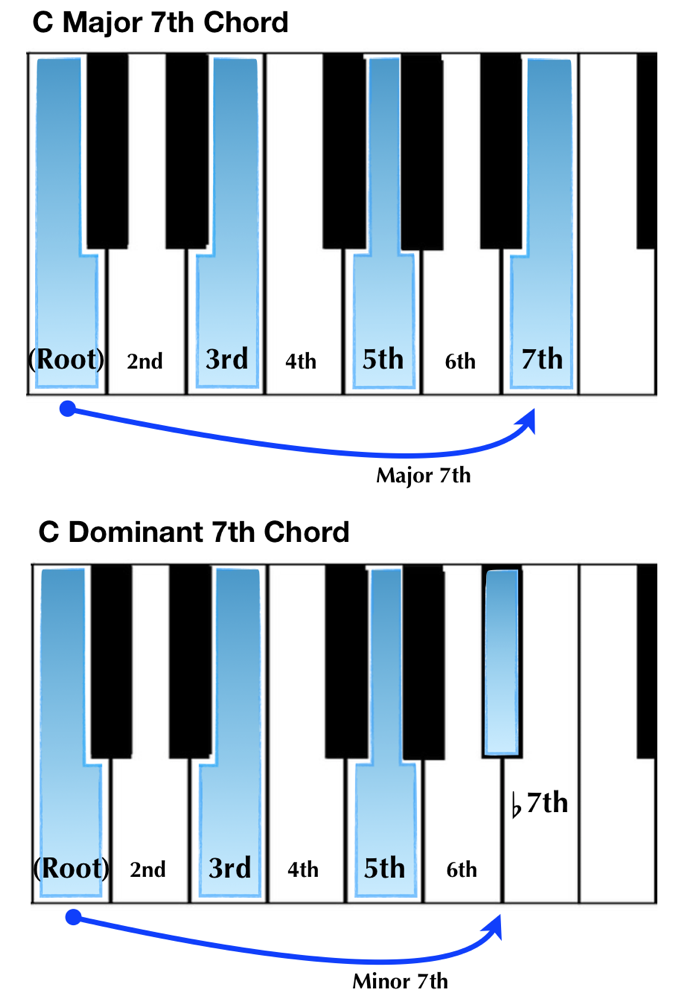
You’re probably wondering about the word ‘dominant’ in the name of the second chord. For now, accept that it is a formal but common term for any time we have a major triad with a flatted 7th. Later on we will learn that there’s more to it, but let’s go with that for now.
When naming 7th chords, we consider the core triad to be major unless we say otherwise. The qualifiers on these chords (‘major,’ ‘dominant’) are referring to the 7th. This is, as much as anything, so that we don’t have to say things like, ‘C Major, Major 7th’ every time we talk about a major 7th chord.
In fact, when speaking informally, we usually leave out as many words as we can when describing these chords. Most notably, ‘C Dominant 7th Chord’ is shortened to C7. To summarize: for any 7th chord, we assume the base triad is major.
Now an added point of convention: we also assume that anything referred to as a (blank)7 (e.g., C7) has a flatted 7th. If the 7th is major (as in, not flatted), we must write it as such.
Occasionally the best way to put a finalizing cherry on top of such a convoluted cake is to present an example with all variables present.
Such as this one:
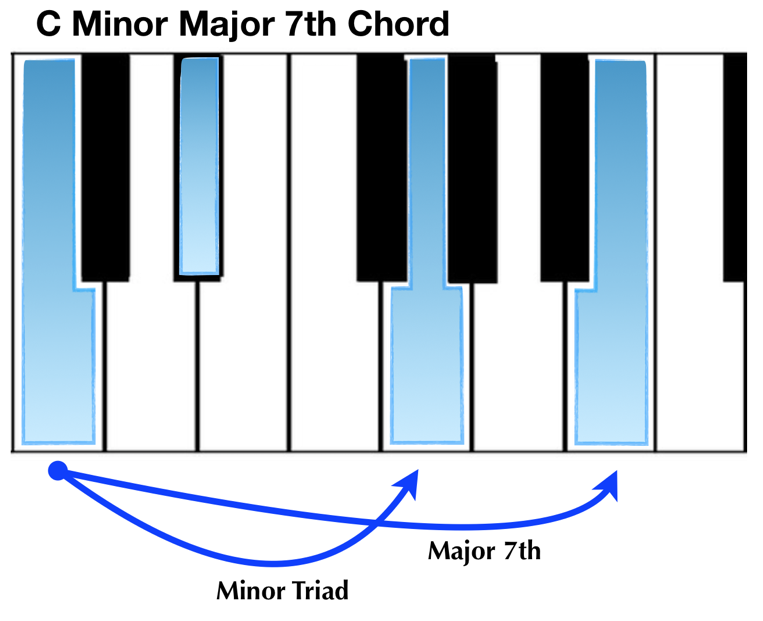
Here we have a minor triad, with a major 7th on top. We need to write ‘minor’ because the chord is not major, and we need the ‘major’ because the 7th is not flatted (dominant).
Let’s reinforce this by flatting the 7th:
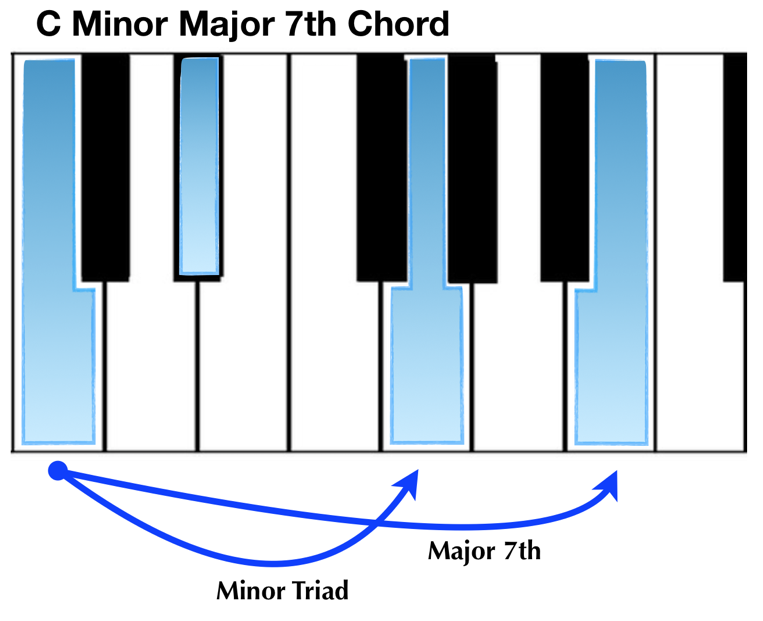
Here our triad is still minor (hence, ‘minor’), but our 7th is flatted so we simply refer to it as ‘7th.’ A common shorthand way to write this would be: Cmin7
Smooth Moves: Chord Inversions
Whew. Way to hang in there.
We have one more structural point to address before we can actually start looking at this stuff in the music…
Let’s look at this next chord on the keyboard:

If you don’t know what it is already, take a moment to use what you learned above to identify it. Go ahead and count the steps to figure out the intervals.
Yes, it is in fact the lovely F major chord, a common counterpart to its somewhat overrated cousin, the C major chord.
Chords by themselves are all well and good, but it's a rare song that is written with only one of them. One of the great joys of music is the experience of being drawn down the musical narrative by shifting harmonies. Think of your favorite piece and your favorite part in it; whether you know it or not, your choice is almost certainly due in some part to something happening harmonically (such as a chord change).
All those shifting harmonies mean shifting hands on our instruments, and at the piano, as with most polyphonic instruments, the degree of hand shifting we have to do is directly related to how hard we have to work to achieve the desired effect.
On our instruments and in notation, the ‘stacked thirds’ version of a chord is known as root position. As we’ve learned, root position is the most basic form of the chord, and the one in which it is most easily identified. If you used the counting methods we just spoke of to identify the chord above, you found out that it was an F major chord in root position.
Let’s move our root position C major chord to our F major chord on the keyboard:
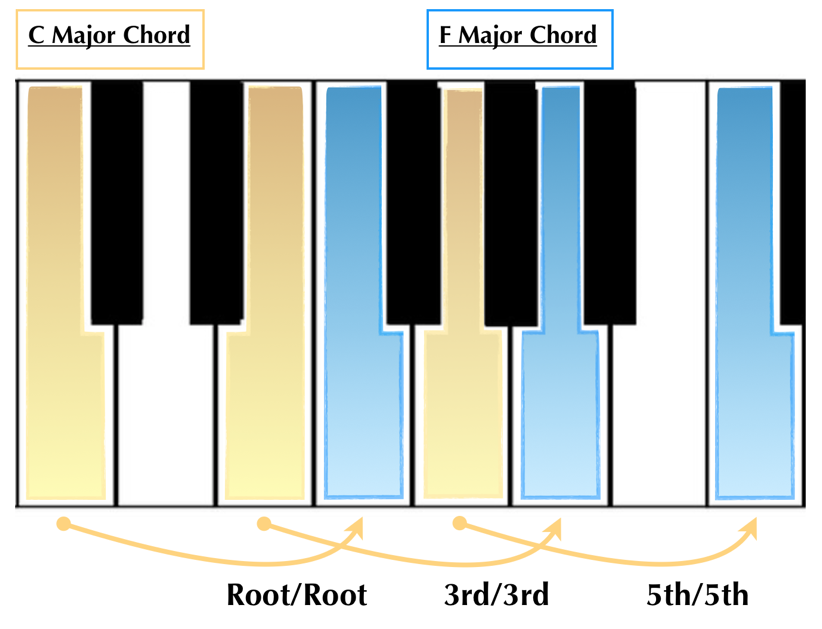
See if you can play this on the piano. Does it feel like a bit of a jump? Imagine being in the middle of a rapid fire section of classical music, or a blazing jazz solo: jumping the hand from one root position chord to another so ‘far’ away is quite the effort.
As it happens, we can achieve the same harmonic feel of a chord even if the notes are not stacked in thirds. Indeed, there is a slight difference in the sound, but it hardly sacrifices the harmonic quality.
Let’s reconfigure our F major chord a bit. How about if we take our C and put it down an octave?:
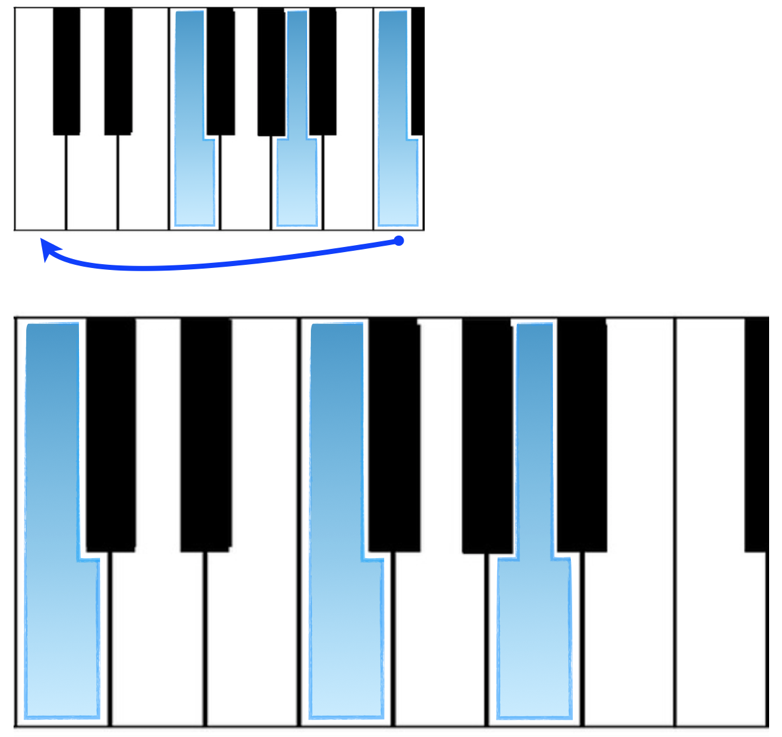
As we still have the note F, A, and C in our chord, it’s still an F major chord. We’ll get to what we call this in just a moment, but for now, let’s go back and see what moving our root position C major chord to this newly positioned F chord looks like:
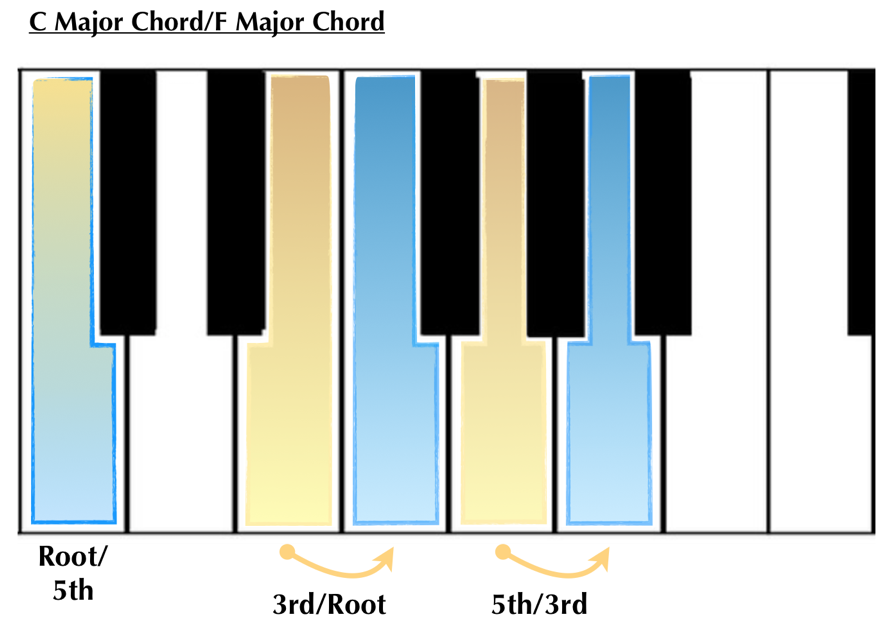
Now we can see that in moving the chord the root of the C major chord has become the 5th of the F major chord, while the third has moved to the F chord root and the 5th to the F chord 3rd. The C has become a common tone between the two of them, requiring us to only move the top fingers of our hand to reach the two new tones of the new chord, instead of our entire hand.
Try this out a few times at the piano.
In moving the note C down to the bottom of the chord, we have changed its inversion. That is to say, we’ve changed its position, in this case to achieve a smoother hand motion. Inversions also generally afford us a smoother transition from chord to chord, which was so important to classical music of old that we now consider it an inalienable part of thinking about that music.
Each triad and 7th chord has as many inversions as it has notes (3 inversions for triads, 4 for 7th chords). We won’t be exploring inversions in depth here, but we will take a moment to learn how they work by looking at the triad inversions.
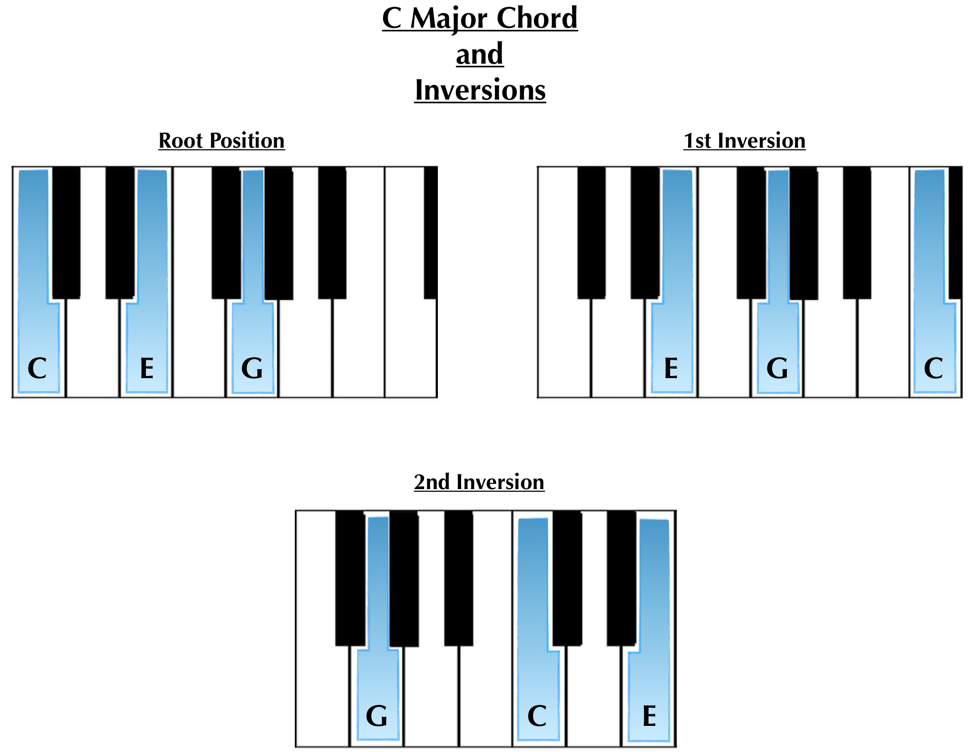
Play each of these on the piano, starting from the root position C chord and moving upwards through 1st and then 2nd inversions.
As with counting up scale degrees or chord thirds, we name inversions by upward position changes from the root position. For each position change, think of taking the bottom note from the previous position and putting it on the top of the chord an octave above.
A helpful tip for finding the root of a major or minor triad in inversion is to find the 4th interval (e.g., from G to the C in either 1st or 2nd inversions). The top note of the 4th interval is the root of the chord, and once you’ve identified that it is much easier to stack the other notes into thirds on top of it. Another helpful thing to try and remember is that in 1st inversion the 4th is on the top, and in 2nd inversion the 4th is on the bottom. It’s important here to note that this method only works if the chord tones are packed as close together as they can be (as seen above). If the notes of the chord are scattered across different octaves above the bass (a technique known as “open voicing”), you’ll need to bring everything back down as close to the bass as possible for this sort of identification to work.
As you might imagine, applying this logic to 7th chords, which have 3 inversions in addition to the root position thanks to their fourth note, is a study unto itself, and a bit more than we need to bite off here.
What’s in a Chord Name?
Now let’s turn to how we refer to these chords in music.
There are multiple shorthands for identifying chords as we see them on the page. These chord abbreviations depend on what the chord is, what inversion it’s in, where it’s happening, what’s happening around it, and what style of music we’re looking at.
The simplest and most direct way of abbreviating a chord is one we’ve already sampled in the paragraphs above, with the naming of the C minor 7th chord (Cmin7). Here are some more examples from that style of chord abbreviation:

Notice that all the chords in this example are in root position. Notice also that the names of the major chords are shortened in writing to simply the note name (in speech it’s still necessary to specify major or minor). In this particular form of abbreviation, we indicate chord inversions by following the basic name of the chord with a slash (/) and then the name of the bottommost note. In this case, while it is still accurate to say that the chord is in 1st or 2nd inversion, the common way of saying it is ‘x-chord over x-note’ (e.g., C minor over G, or G over D).

Particularly for non-classical style musics, this kind of designation tends to better reflect the ways in which the players are thinking about the music.
Important to know here is that there really isn’t a codified format for chord abbreviations. You may see different versions depending on the sources you’re viewing and type of music your looking at. For example, a C minor chord can be written as Cmin, Cm, or C- (yes, as in minus…).
Figuring Things Out: Seeing Chords in Music
As we progress in our learning about keys we will learn more about chord designations. In particular, we will learn how chord designations can actually reference the keys we may be playing in in very significant ways.
For now though, let’s keep moving and take a look at this simple tune:

Ahh…if only all chords could be so clearly seen. (By the way, the ‘dim’ in the ‘Bdim’ chord is an abbreviation of ‘diminished,’ which is one of the non-major or minor triads we saw earlier.)
Music would be missing most of its character if the only way harmony was expressed was in the fashion of the example above. To be sure, we love our bass/chord/melody type songs (think of Gershwin and so much of Romantic music), however for many types of music, this kind of execution is more of a blueprint than a finished product. As was mentioned at the beginning of this article, the concept of the ‘chord’ or of a harmony structure that was anything other than a happy mingling of multiple melodies really wasn’t even considered until Bach’s time. Even then, the thought of leaving chords as they were, bereft of any sort of elaboration, was nearly unthinkable.
Here are some more chords for you:

Notice that we have some repeated notes in some of the chords (in blue), which is called doubling. Doubling does not change the quality of the chord, and, if done well, can add a tasteful emphasis or a powerful reinforcement.
All well and good, but it’s still a simple chord progression (a what? more on that in a moment). In the master hands of Bach though….

Being able to distill sections of musical material down to the chordal harmonies within them is one of the most valuable skills a musician can have. Particularly when learning classical music, the ability to ‘see the chords through the notes’ can make even the most visually frightening passages seem at least understandable. Consider the following:

Ok fine, maybe it’s still a little terrifying…
As we can see, each of these mighty arpeggios is simply an ‘exploded’ version of some fairly simple chords. As is often the case in such examples, the representations are not always pristine (you may notice that the F’s of the Dmin chord, in orange, have sneaked down into the C chord material), however it is generally much easier to think of these kinds of figures as blown up chords with a few elaborations in them than on a note-by-note basis. By the way, the ‘pedal’ featured in this passage refers to a note, usually the root of another chord, that hangs out while other chords move over it.
Alright, alright, how about something like this:

Which Mozart takes and turns into this:

That’s right, it’s our good friend Sonata No. 16 in C major, K. 545 from the opening article of this series! This breaking up of the chord is a kind of figuration, which might be best defined as a way of breaking up chordal tones into phrases that give character and identity to the music. This particular sort of chord figuration is known as the Alberti Bass (named after the composer Domenico Alberti, 1710—1740/46) and while Mozart did not invent it, it is perhaps best known today as a common feature of his keyboard music.
There are many different ways of breaking up chords to enrich the musical identity of a piece. Often, however, our quickest way of learning is to put the notes back in place so that we can clearly see the intended harmonic picture before scattering things back into their musical form.
Sweet Moves: Chord Progressions
We have one more basic feature of chords to touch upon before we are ready to start thinking of them in terms of keys.
See if you can play the following excerpts at the piano. They need not be played quickly, but try to see if you can get them steady enough to hear the effect of the chord changes as they pass from one to another.

It should go without saying that one of these sounds more strange than the other.
Why do you think that is? They obviously consist of different chords, but they do both use only ‘white’ notes, so why does one sound so off in comparison to the other?
Let’s take the scenic route to answering this...
Do you ever wonder how there can be so much music in the world? Especially once you begin to learn about how music is built and what components go into building it, it’s a little astonishing to think about how much music there is and how different one piece can sound from another. Different orchestrations and digitally edited music notwithstanding, even simply the universe of piano music contains a vastly varied repertoire.
Look at the following series of chords. The first example consists of root position chords, while the second consists of inversions of those same chords.

Playing this at the piano, we feel that it shares the qualities of top progression seen above over the bottom one, which is to say, it seems like a nice progression of chords. Indeed, as you’re no doubt already aware, the chords we may hear in a given piece are not typically random. Chords generally occur as part of a harmonic pattern or narrative that makes musical sense or is musically satisfying.
We refer to the musical narrative of chords as the chord progression or chord changes (both of which are commonly shortened to ‘the progression’ or ‘changes’ respectively).
Chord progressions often follow specific, musically structured routes depending on the style of music. In other words, pieces from any of the many eras of Western classical music, jazz, pop, or any of a number of other genres will often work with semi-standardized combinations of chords to help achieve their sound. Interestingly enough, many of these ‘common’ chord combinations cross the boundaries of both time and genre such that they can be found in different kinds of musical settings, sometimes separated by hundreds of years.
Were we to try and compose a sonata in the style of Mozart without employing the chord progressions that would have been common to use at Mozart’s time, the results would sound awfully strange. The reason the two different chord progressions above are so different is because one follows some of the general guidelines for how a ‘good’ sounding progression should be built, and the other is largely random. It’s worth reinforcing the point here that there are many styles of music that use many different types of chord progressions, and many of them sound quite different than anything seen here.
In combining our knowledge of how chords are built, how their numerous variations function, how they can be broken up and identified through musical figures, and how they tend to move from one to another in established musical trends, we are ready to start digging into the heart of how we can use chords to think about keys. In our next article, we will take the knowledge of harmony we’ve gained in looking at chords, the knowledge of melody we gained in investigating scales, and blend the salient points of both towards directly looking at keys, how they work, and how they can work for us.







