Applying Scales and Chords to the Study of Keys
From the beginning of this series, we set out to achieve a succinct but comprehensive understanding of what keys are and how they can help us in our musical pursuits. We started by presenting a common musical scenario heavily dependent on keys for its construction and learning potential (in this case, a snippet from Mozart’s Sonata No. 16 in C major, K. 545). We then highlighted some of the most basic infrastructural components we find in music (chords and scales) for the sake of reinforcing the knowledge base we’ll need to understand keys from the ground up. We simplified things even further in investigating the building blocks of each of those components.
Now, we are ready to apply our learning effort directly to the question: What are Keys?
We will compile our answer to this question over three primary articles:
In the Discovering Keys: Applying Scales and Chords to the Study of Keys, Part I article, we will apply our refreshed understanding of chords and scales toward our study of keys. We will show how the effort put into learning how chords and scales are built, named, and found in music pays off in using them to help us understand keys.
In Discovering Keys: Applying Scales and Chords to the Study of Keys, Part II, we will delve more deeply into what to look for in identifying keys, and how we can use the knowledge of what’s not in the common components of keys to figure out how they’re functioning. We’ll also look at how we can maneuver within keys for greater effect, and how we can modulate—or change—from key to key.
In our final article, Discovering Keys: From Then to Now, we will look at some real-world applications of keys, and explore how we might further our study of them as we continue down our musical paths. We will provide some historical overview, look at musical examples across a number of genres and settings, and consider how we can get the most out of our knowledge moving forward.
In addition, we’ll take a detour into the wonderful, but slightly more complicated world of minor keys in a special article dedicated to them, Discovering Keys: Minor Keys.
The Road So Far: Our Friend Mozart
As we will very soon discover, one of the most valued aspects of thinking in keys is the artful return.
With that in mind, let’s take a look at the sonata snippet from our friendly master Mozart, which we introduced in the opening article of this series.

Go ahead and give it another listen. This link will take you to a great rendition by a very young Yuja Wang. If you have yet to become familiar with her, look her up; she’s come quite a ways since this video…
If you’ll recall, we presented first the version above, bereft of any edits or analysis, and then a second version in which we added some color-coded highlights and analytical symbols in the attempt to emulate how a musician with a knowledge of keys might view the work:

The Road So Far: Scales
To briefly recount, our goal here is to provide a visual representation of the melodic and harmonic content that is relevant to thinking about this selection in terms of keys.
In our article on scales, we reviewed scale construction and took our first steps towards perceiving scales as the basis for the melodic and harmonic identity through which keys are defined. We learned how to name scales using both numbers and the musical phonetic language known as solfeggio. We also learned that the identity of a scale is based on the combination of steps between notes. For example, the combination of steps for the major scale starting on C are as follows:
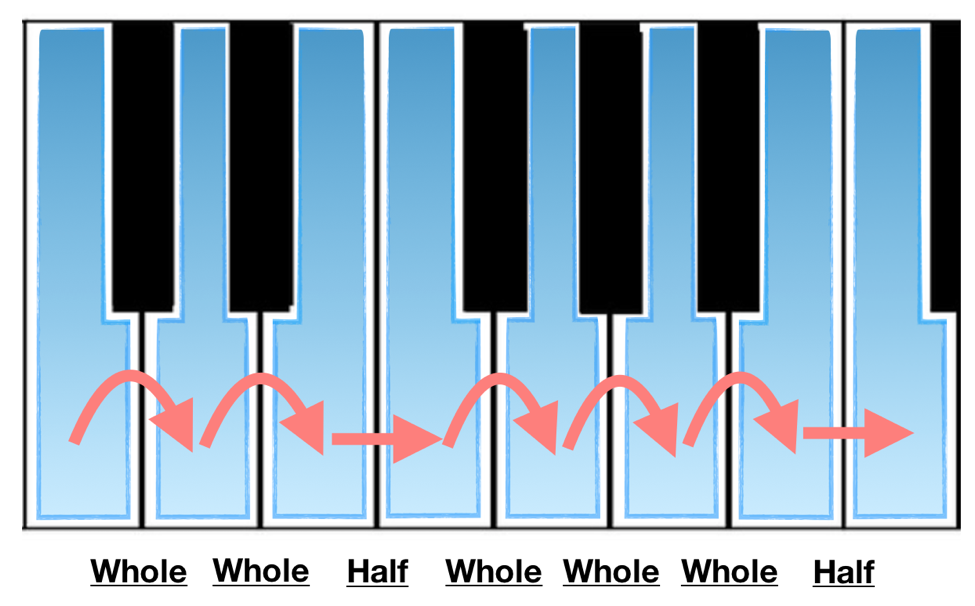
Additionally, this can be abbreviated as: WWHWWWH
We introduced the tonic of the scale (the ‘1’ or ‘do’ note) as having a special significance for how the notes of the scale relate to one another, and emphasized the order of scale steps as integral to the sound of a scale and to the sound of the music for which that scale is serving as the groundwork.
As an example, almost every note in the Mozart sonata excerpt above falls within the C major scale, however it is Mozart’s arrangement of those notes that informs us that this opening section of the piece occurs within the key of C major (as it would for any musician of this stylistic era)
Recall too that it is possible to have the notes of a scale present without demonstrating the identity of the scale. Remember this little gem of a rendition of Twinkle, Twinkle, Little Star?:

The notes are those of the C major scale, but because the tune starts on an E instead of a C, the order of steps between the scale degrees is subverted, and we do not hear it as taking place in the C major scale.
From the perspective of scales, this concept of the importance of the tonic is at the heart of thinking in keys.
The Road So Far: Chords
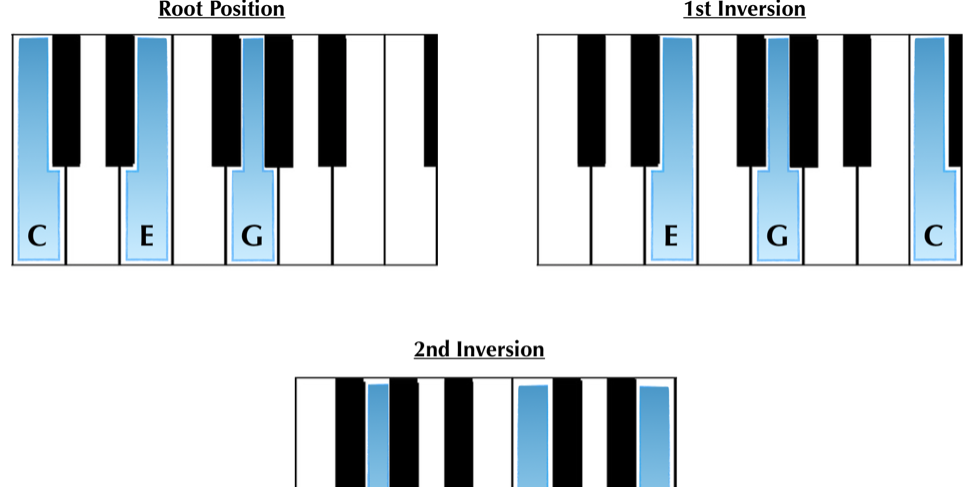
In our article regarding chords, we reviewed basic chord construction, chord nomenclature, and touched on the importance of inversions, chord progressions, and the ability to distill chord identities from musical figuration. We learned that the basic structure of chords consists of stacked thirds, and that to identify chords we need to find their root and be able to build them in root position. We also learned how to name chords, and how to identify chords in written music with chord abbreviations.
Applying our knowledge of chords, we can now analyze the opening of the Mozart sonata like this:

We ultimately use the combination of these interpretations when identifying the harmonic scheme and structure of the pieces we’re studying.
Before we continue on to the meat of translating our knowledge of chords and scales into thinking of keys, let’s do one more application of the salient points of chords and scales on a fresh piece just to reinforce our understanding.
Here is a link to a recording of this piece by the eminent pianist Sviatoslav Richter

Learning Keys: Scales
Undoubtedly, the first identifiable trait of any key we will be looking for, will be what scale it uses. This is where most of us first learn how to think about keys as beginning students. It is also where most of the confusion is sewn when we come back to keys as more experienced students—to discover that keys are so much more than their scales. This is not to say that figuring out the scale of the key we’re in is not an important aspect of identification (indeed, it’s probably the most important step right out the gate), simply that there is much more to what keys are and much more that we can glean from having a deeper knowledge of their use.
All that said, let’s start by looking at some of the more obvious ways we can identify the scale of a key.
The first and by far most relied upon method is to know the key signature. The key signature is the collection of accidentals (sharps or flats) that we see beside the clefs at the beginning of the piece:
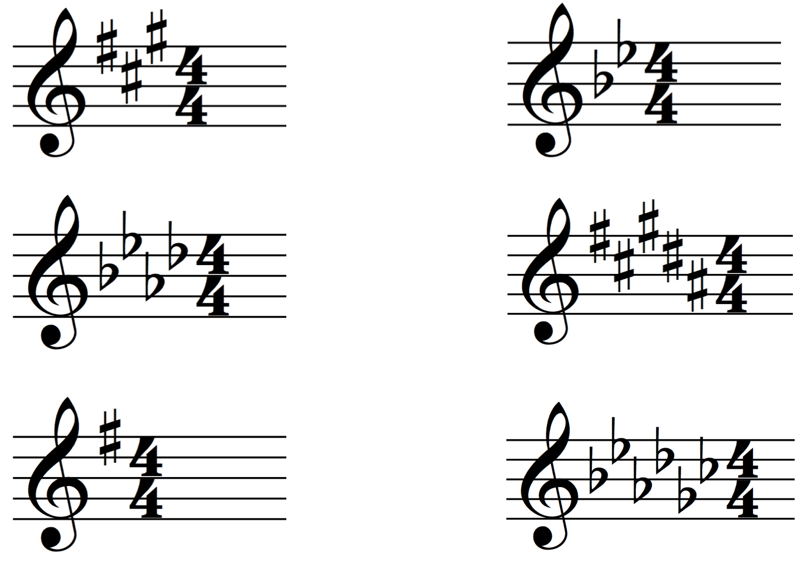
The key signature is a shorthand method for indicating which notes in the scale should be sharped or flatted. All notes of the scale, no matter the register, are affected by the corresponding accidentals in the key signature. So, for example, if we have a C-sharp in the key signature, it indicates that every C we play will be sharped unless otherwise noted. Without the key signature, we would have to write in each accidental for our scale each time it came up in a measure.
The examples below show a passage from Mozart’s Sonata No. 11 in A Major, K 331, first without a key signature (i.e., with all of the necessary accidentals written in), and then how we would see it on the page when using a key signature:

Using a key signature accomplishes two things for us: it allows us to avoid having to look at lots of accidentals when reading music, and it narrows down the key possibilities for us at the very beginning of the piece.
The trick here is knowing which scale corresponds to which key signature.
We can start by knowing that keys will always use either a major or a minor scale. There are other scales in the musical world (many others, in fact), however, when playing key-based music, we can always count on having our base scale be either major or minor. Thus, we need to know which number of sharps or flats go with which scale. It is here that we can use one of the more recognizable and misused tools in music: the Circle of 5ths.
The Circle…of 5ths
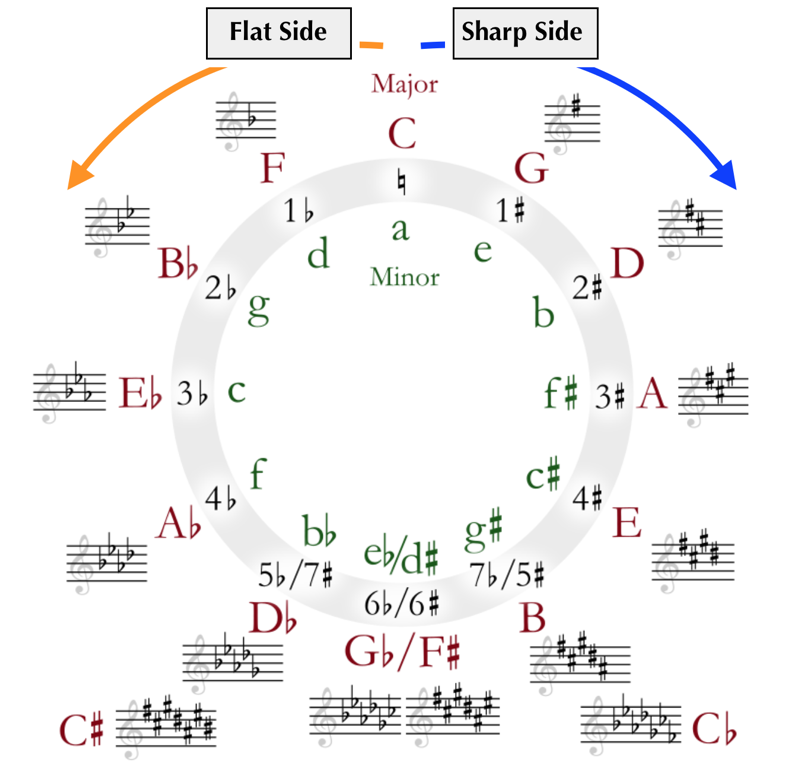
The Circle of 5ths is a commonly seen diagram that is helpful for identifying scales and mapping out the distances and relationships between scales. Likely the most obvious thing you’ll see as you look at the Circle is the letter names and key signatures circumnavigating the rim. These are our major scales and their corresponding key signatures.
Take a moment to play the ‘1’ or ‘do’ note of each scale (the tonic or root) upwards from middle C (so, play middle C and then up to G and then to D, etc.) until you get as far around the Circle as you can with the sharp-based key signatures. Now do the same with the flat key-signatures going down.
At this point you may be asking, why 5ths?
The answer to this question is one of acoustics and harmonics and all sorts of wonderful, natural musical phenomena dealing with the physics of sound waves. It is also a bit beyond the purview of this article, however let’s see if we can give you a quick explanation via an example on the piano.
Try this:
Go down to the bottom register (if you’re using an older or more out of tune piano, you may need to use the octave above the lowest register to get the best version of the effect we’ll be looking for). Find the interval of a 5th (the one between G and D works well for this). Play the two notes together. This works best if you give them a good forte strike and hold. Listen not so much for the notes themselves but for the quality of the sound. Play this several times to get it in your ear.
Now play your lowest note with a note a half-step above (if you’re using the G that note will be Ab).
Wow. What a difference, yes? Flip back and forth between playing the 5th and the minor 2nd and listen to the qualities of the two sounds. To be sure, you may find both sounds unpleasant, however something in the nasty, gritty, pulsating quality of that low minor 2nd should really stand out between the two.
This difference in quality is because the interval of a 5th is inherently more ‘smooth’ on the harmonic spectrum. That very distinct vibration you’re hearing in the minor 2nd is the clashing of harmonics--the sound waves, and it is significantly less intense in 5th intervals. This make moving from one 5th to another much more smooth harmonically, and also means that moving scales by 5ths sounds much more smooth in practice.
Let’s get back to looking at the Circle.
The most simple use of the Circle of 5ths is to compare the key signature you’re seeing at the beginning of a piece with the corresponding location on the Circle:
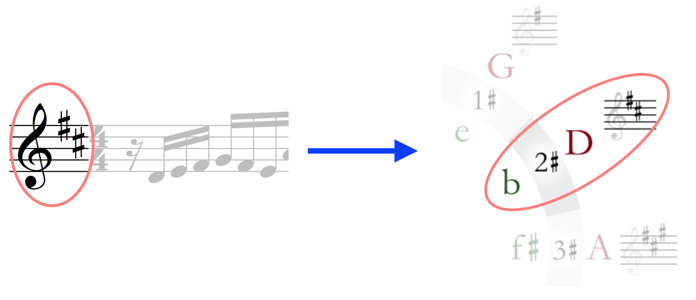
Notice that on the inside rim of the Circle we see lower case letters coupled with the heading ‘minor.’ Think this might have something to do with minor scales?
Indeed it does. For every major scale, we have a sibling minor scale that utilizes the same key signature.
This is part of the reason why it’s not enough for us to simply see the key signature in the piece and link it to its major scale on the Circle; we also need to know whether the key signature is being used for the major or minor version of the scale.
There are several versions of the minor scale. The one we’re speaking of is known as the ‘natural minor’ scale, which is built by flatting the 7th and 6th of the major scale in addition to flatting the 3rd.

When we change a major scale to a minor scale but keep the same tonic (as in the example above), we call this a parallel relationship (i.e. C minor is the parallel minor of C major).
In using the same key signature to identify major and minor scales, we need to find the scale location that uses the same number of sharps or flats. Fortunately for us, this location is always the same: If we’re trying to find the minor scale that uses the corresponding key signature of a given major scale, we must go down a minor 3rd interval, and must do the opposite if we’re trying for the same thing from minor to major.
Yes, let’s look at a quick example:

Here we can see how the scale of A natural minor scale also contains no sharps or flats. We call this a relative relationship (i.e. A minor is the relative minor of C major). Try playing these both at the piano.
Let’s look at one more similar example so that we can confirm what this looks like for scales in a key signature with more accidentals. Below is the A major scale with its companion relative minor scale, F# natural minor:

Another thing you may have noticed on the Circle is the overlap of sharps and flats towards the bottom. As we accrue accidentals, either sharps or flats, we will eventually get to a point at which we need to use double flats or double sharps to accurately name the scale tones. As an example, to get the half-step between the 7 and 1 scale degrees at the beginning of the next scale up for, say, the scale of D# major, we would need a C double-sharp. At this point, it is much easier to recognize that D# is enharmonically Eb, and that building the major scale as an Eb major scale is much easier.
We also mentioned earlier that the Circle of 5ths, in addition to being one of the more recognizable tools, is one of the more misused tools we have in music. Why is this? Much of it comes down to the conception of the Circle as an explanation of keys unto itself. It is not. The Circle of 5ths is simply a helpful guide for identifying the scale possibilities for given key signature, and a diagram of how key signatures relate to one another via the smooth, consonant relations of 5th intervals.
The Circle does not show us how components within the key relate to one another. For that explanation, we need to move on to our next section, in which we we start to apply our knowledge of chords to what we’ve learned so far.
Learning Keys: Chords
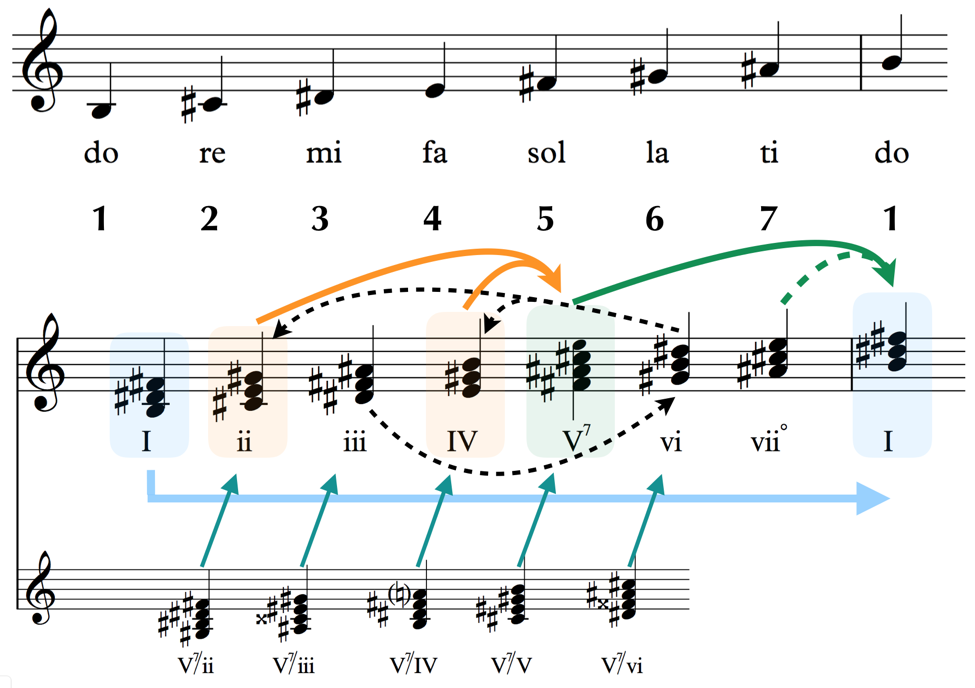
Long ago in an article far, far away we presented to you this rather perplexing looking visual:

It probably doesn’t look much more decipherable now than it did the first time, however you can probably pick out the structures of scales and chords, even if their identities as a whole are still obscure.
What you’re looking at is a micro-version of the theory of keys as a music theorist might think about it. Encompassed in these strange structures and esoteric arrows is much of the information inherently built into keys as we hear them used in a vast amount of Western-style music. Don’t worry, we’re not going to get too crazy trying to understand all of this, however we are going to pull a couple of essential features that will make our investigations into keys more fruitful.
One of the more visually striking features of the example above is the long line of chords going up what looks to be a scale in C major. Let’s break it down a bit and give it a look in a somewhat more more familiar context:

As might seem appropriate, we call this a chord scale, and it serves us well as a connecting path between the theory of scales an the theory of chords as they relate to keys. For this example, we’ve stripped away any auxiliary symbols and additions, leaving only a cue-sized version of the commonly used dominant 7th on the G chord in what is otherwise a very basic chord scale on C major.
The chord scale is among the most important tools we have at our disposal for thinking about keys and how they work. It shows us how we can create chords on each scale degree, and how we can thereby provide harmony to any melody that is happening in that scale.
We’ll talk about why this is so important to think about when considering keys in a moment. For now, try playing the chords scale in C major presented above at the piano. Can you identify each triad?

Towards the end of our article reviewing the construction and basic use of chords we started to talk about chord progressions, which we defined as the harmonic narrative underlying many forms of Western-style music. Most styles of Western classical music, jazz, pop, rock, and other styles depend on chord progressions to give harmonic life to their melodies and rhythms. If you’ll recall, chord progressions tend to follow certain designs, which is another way of saying that some movements from chord to chord sound much better than others depending on the style of music they are being used for.
Let’s look back at a few of those examples of chord progressions:

Recall that both of the lines above show off essentially the same progression, with the top line simply being a depiction using root position chords, and the bottom line being one that uses inversions. Whether we’re looking at the root position version or the inversion, I think we can agree that this is a fairly decent sounding sequence of chords (a nice chord progression, if you will). You may already be seeing this coming, but let’s go ahead and compare the root position progression to the chord scale we just looked at in C:
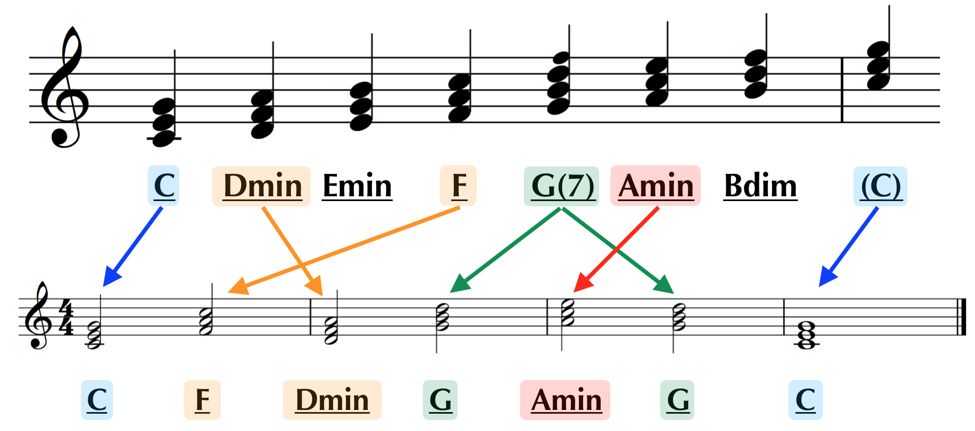
As we can see, all of the chords in the progression are represented in the chord scale, and almost all of the chords of the chord scale are represented in this progression; the only absent chords being the E minor and B diminished (which could very easily have made it in as well). Notice in the second line of this progression how the G major chord becomes a G7 chord in inversion (albeit one that’s missing it’s 5th, which is a common omission in this case).
While it would be useful to simply have the chord scale exist as a compendium of available chords for a given key, its true value comes in how we think about using the chords it presents. When thinking in keys, we assign values and relationships to the chords within the chord scale, and it is this manner of thinking about the chord scale that really lets us get to the heart of keys, what they’re about, and how they can help us.
What’s Your Function?
In the decades around the turn of the 19th century, an Austrian born composer, theorist, and educator named Heinrich Schenker (1868–1935) developed a method for analyzing the structures and musical habits of the music of what is known as the ‘common practice’ period of Western classical music (basically, from Bach through the late-romantic composers). At its core, this method, known as Schenkerian Analysis, posited that music based in keys (such as that of the composers from the common practice period) was geared around an elaboration of the tonic triad, which we can also think of as being the tonic note or home note. Through this manner of thinking, all of the notes and chords featured within the scheme of a given key have a priority-based relationship with the tonic, and, as a result, with each other. We say that these relationships give chords function or functionality, and that, friends, is what thinking in keys is all about.
Whew again. Way to hang in there. Let’s make some sense of all this.
To begin, let’s clarify that this is not an article about Schenkerian Analysis. We will borrow some of the relevant tools from Schenkerian Analysis, but the theory itself is a bit advanced for us at this point. Fortunately, the basic tools we can borrow from Schenkerian Analysis are easy to work with and can be applied to a broad spectrum of musical contexts.
There are two primary facets of Schenker’s theory that we can cherry-pick for our purposes. First is the notion that the tonic triad or home note is the beginning, end, and most highly prioritized aspect of the chord relationships within our key. Second is the system of naming chords within the chord scale so that when we identify them in the music, we have a distinct role and position in mind for them within the greater harmonic scheme (within the chord progression, if you will).
These two things together constitute the primary principle and procedure behind the concept of functionality, and once we can confidently grasp the basics of what they mean and how they are used, we will have a solid grasp on what keys are all about.
Let’s talk about the naming first. If you glance back at the dreadfully convoluted looking image of the chord scale with all the arrows and colors we displayed earlier, you might have noticed the Roman numerals under each chord. Schenker designated these Roman numerals to the chords in the chord scale in a way similar to how we designate numerals or solfeggio syllables to the basic scale. The main difference is that the Roman numerals indicate much more about a chord than its position in the scale.
On a purely practical level, the Roman numerals tell us the scale degree and quality of the chord to which it is being assigned.
Let’s look at the chord scale again, but now with the Roman numerals assigned to their respective chords within the C major chord scale.

As we can see, the Roman numerals have been applied with the capital ‘I’ numeral starting off our tonic triad, and the remaining numerals progressing up the scale just like our Arabic numerals would for a regular scale.
What, you may be thinking, is the difference between using the standard chord abbreviations and the Roman numerals? The answer to that very good question is twofold.
First, the capitalization of the Roman numerals is actually an indicator of a chord’s core identity (whether it is major or minor). An upper-case Roman numeral indicates a major chord, while a lower-case Roman numeral indicates a minor chord. (As an aside, it’s more accurate to say that the upper and lower cases refer respectively to major and minor thirds from the root of the chords, as we also can use an upper-case Roman numeral to indicate an augmented chord and a lower-case to indicate a diminished chord.)
This ability to identify the major or minor quality of a chord via the capitalization of its Roman numeral is an effective shorthand that avoids some of the shaky practices of standard chord abbreviation.
The second difference is a bit more conceptual, but really represents the core of thinking of keys and the idea of functionality.
Whereas standard chord abbreviations can be applied to any chord with the requisite chord qualities within any context, the Roman numeral assignments in a chord scale are tailored to the key that chord scale is serving as an infrastructural part of. Put plainly, a D minor chord in the key (and consequent chord scale) of C major will only be a ‘ii’ in that key. If we find it as part of another key, it will have a different Roman numeral assignment, and a different function as a part of that key.
Let’s look at a couple of different chord scales that feature a D minor chord. Notice how the Roman numerals for the chord are different depending on its position in the key:
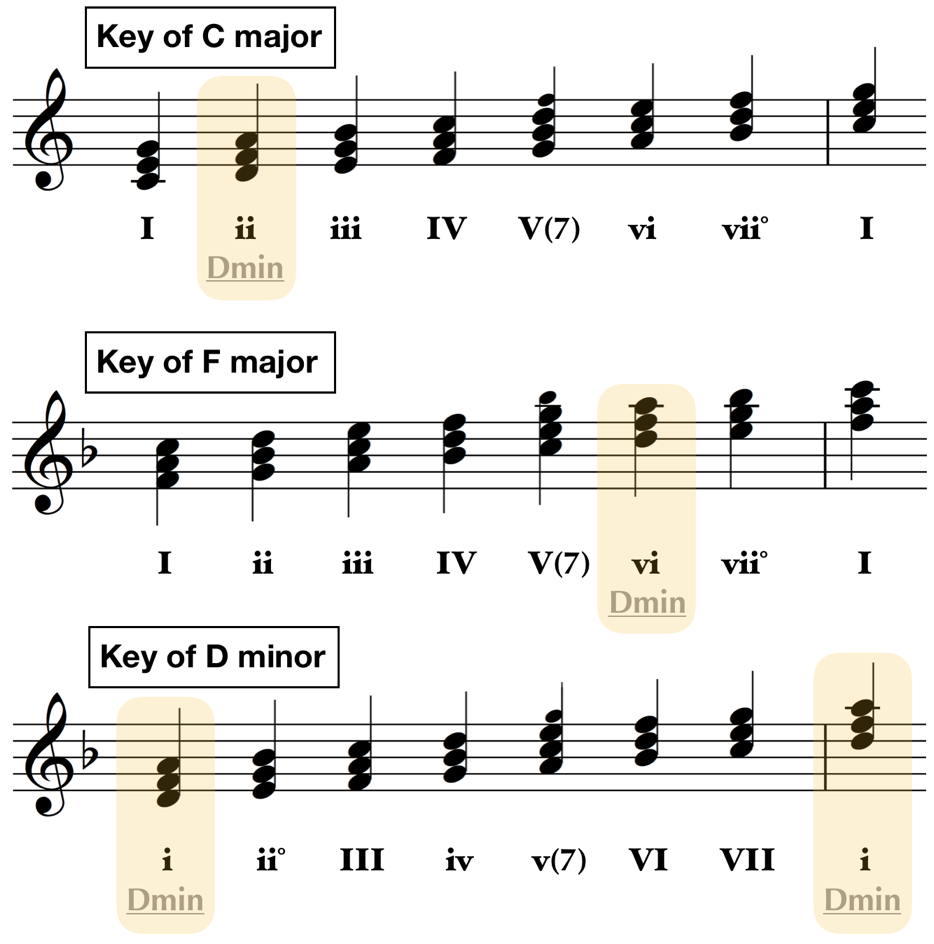
The real trick here is to understand that a ‘D minor’ chord is always a ‘D minor’ chord no matter what, but a ‘ii’ or a ‘vi’ has a identity within the key. Chords identified via Roman numeral have a relationship with the chords around them and with the chord progression they are a part of. They usually occur at a certain points in the music, and accomplish a specific sound and feeling by occurring as such.
If we look at the music from which these concepts are derived (so, music that uses keys) we consistently see the Roman numeral functions (that is, the chords we have assigned Roman numeral designations to) coming up in the same spots and being used for similar purposes. We see that iii’s like to go to vi’s, iv’s like to go to IV’s or ii’s, IV’s like to go to V’s, and, most importantly, V’s like to go to I’s.
Play the following at the piano:

Traditionally, what you just played is the real indication that we are in a key, and not simply using a major or minor scale in some other musical context. That sound, that feeling of the ‘V’ chord of a chord scale going to a ‘I’ (or i, if we’re in minor) is the governing musical maneuver behind a tremendous amount of music, old and new alike. We’re hearing it constantly, in almost all forms of music, and, more importantly, are seeking to hear it in music we naturally understand to be working in keys.
We call this move the cadence, and while it comes in many varieties, it is primarily found as some form of V - I, or, dominant to tonic relationship.
Now, in our final section of this article, let’s look deeper into what the cadence is, what it means, and how it affects the music that is built in support of it.
Five-One
Look again at the first two measures of the annotated Mozart excerpt from the beginning of this article:
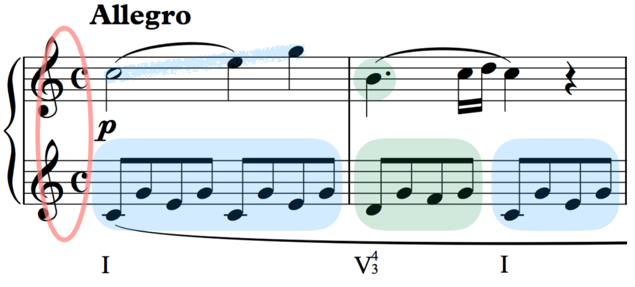
Do the Roman numerals underneath each chord make more sense now? The numbers next to the ‘V’ are indicating a chord inversion. If you’re wondering why they look familiar, it’s likely because we sampled them very briefly in the beginning of our ‘Chords’ article in this series, when mentioning the ancient ‘figured bass’ style of chord abbreviation. Indicating inversions like this is still very relevant to this manner of chord identification.
Notice how the melody here sounds like a complete little phrase, and how it’s built over a very simple cadential chord structure like the one we saw a moment ago. This little cadential beginning is Mozart’s way of introducing and enforcing the key of the piece by going right to its most essential chord progression.The intent is further fortified when Mozart combines the first phrase with its follow up:

In the second phrase we see a slightly longer form that goes from a IV chord F major back to a I and then to our V - I (G7 - C) cadence. This slight elongation and differentiation gives us just enough pull away from the I chord (from the tonic chord) for us to feel the reinforcement of the second cadence before we move on to other things.
This is essentially how music in keys works; we start at the tonic, we go somewhere else, and then we return to the tonic at the end--the artful return.
True Schenkerian Analysis contains all sorts of crazy names for almost every aspect of the key and chord scale, but here we’re really interested in the most commonly heard and used, the two terms dominant and tonic.

Once again, try to think of the dominant to tonic relationship as less a theoretical analysis and more of a feeling in the music. Truly, that is where all of the this comes from - how it sounds in the music.
The trouble for students new to thinking about keys in this fashion is that it can be hard to reconcile adding all of this extra information to what beforehand seemed like such a simple, wonderful world of music simply working. The thing is, outside of living circumstances that are devoted to absorbing music through environmental exposure and hands-on experience, it can be challenging and inefficient to try and learn about keys and how they work in music without information akin to this.
And make no mistake, we can apply the theory of keys everywhere, even in places that might seem too simple to bother applying it. Remember our Twinkle, Twinkle, Little Star example? Well, if we flesh it out with some very basic, sensible harmony, and then show the Roman numeral analysis as it would apply to the key of C major we get:

I know. It’s kind of depressing.
But also amazing.
By the way, the B diminished chord is colored off-green here because vii’s are actually kind of Dominant too, but don’t worry about that for now. We’ll address more of all of this in our next article in the series.
Also by the way, did you know that Mozart actually wrote a famous arrangement of this tune? He wrote it as a ‘theme and variations,’ which is a style of piece in which a theme (usually a popular theme) starts off as a simple rendition and then gets repeated into ever more elaborate and colorful versions.
While it would be inaccurate to say that all music employs cadences, they are a deeply essential aspect to most key-based music. Historically, we have to span about 300 years of Western musical history between when keys first started being really used in their common form and when we first start to see composers attempting to write music outside of them at the end of the 19th century.
In a way, most of Western music history can be described by its relationship to the cadence, and as we trace that trajectory forwards in time from the end of the Renaissance Era we find composers trying harder and harder to find new paths to the cadence, trying to delay its arrival, trying to obfuscate it in textures and musical feints, and, finally, trying to escape it altogether.
Pretty remarkable, yes?
Coming up in Part II of this series, we will explore the relationship between keys and chord progressions, spend some time illustrating the different ways non-scale tones can affect how we think about our keys, and talk about what it means to move from one key to another and how we might recognize that.







Hi, I really like piano and now looking to learn it. Is it a good idea to learn with the help of an online resource like this piano course. Please tell should I go for it? Please also share any good piano program if you know about a good one for beginners or should I take piano classes? But the thing is piano classes are very expensive.